Kontynuujemy temat podjęty w poprzednim wydaniu „Nowoczesnego Warsztatu”. Tym razem skupimy się na zachowaniu koła, gdy naciskamy na pedał hamulca z określoną siłą.
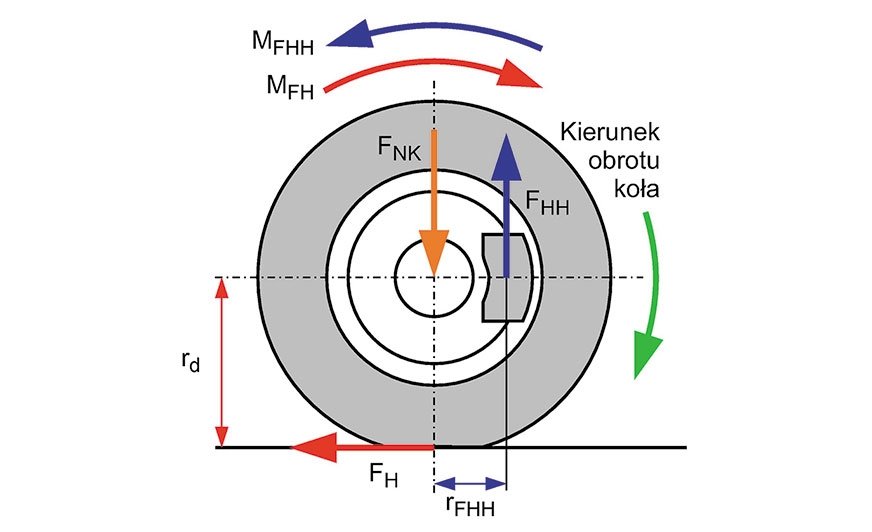
Gdy kierowca naciska na pedał hamulca, na styku materiału ciernego i tarczy lub bębna hamulcowego powstaje siła hamowania hamulca FHH (rys. 9). Ta siła działa na ramieniu rFHH, co powoduje powstanie momentu hamowania siły hamowania hamulca MFHH, którego wartość obliczamy z poniższego wzoru:
MFHH = FX ´ rFHH
Gdy koło jest hamowane, na styku opony z nawierzchnią drogi działa siła hamowania FH (rys. 9). Działa ona na tzw. promieniu dynamicznym rd, którym nazywamy odległość osi obrotu koła od nawierzchni drogi. W ten sposób siła hamowania FH powoduje powstanie momentu hamowania siły hamowania MFH, którego wartość obliczamy poniższego wzoru:
MFH = FH ´ rd
Momenty sił MFHH i MFH mają przeciwne kierunki działania. Jeśli ich wartości są równe, wówczas równoważą się (rys. 9). Mówimy wówczas o hamowaniu w warunkach równowagi. Są to warunki pożądane.
Jeśli tej równowagi nie ma, wówczas tak zmienia się wartość poślizgu koła, aby tę równowagę osiągnąć (jest to tzw. autoregulacja), choć nie zawsze jest to możliwe. Jest to temat następnego podpunktu.
Podstawowe przebiegi hamowania koła
Omówimy trzy typowe przebiegi hamowania pojedynczego koła przez układ hamulcowy bez ABS. Są one podstawą do poznania zasad pracy tego układu i korzyści, które wynikają z jego stosowania.
Dla uproszczenia rozważania w odniesieniu do wszystkich przykładów przyjąłem, że:
- dotyczą koła nienapędzanego;
- koło porusza się po nawierzchni, którą charakteryzuje typowy przebieg zależności współczynnika tarcia wzdłużnego opony mW od poślizgu koła PK, przedstawiony na rys. 5 (patrz część pierwsza artykułu: „NW" 6/2018).
Przy analizie przykładów pamiętajmy, że w „mechanice” nic nie dzieje się natychmiast. Koło ma określoną bezwładność, a ściślej – moment bezwładności. Trzeba chwilę poczekać, aż wzrośnie jego prędkość obrotowa przy przyspieszaniu lub zmaleje przy hamowaniu, nawet jeśli te chwile to ułamki sekund.
Gdy koło nie jest hamowane, ale się toczy (rys. 10a/1), wówczas poślizg koła PK i współczynnik tarcia wzdłużnego opony mW mają wartości zerowe (pkt 1 wykresu na rys. 10b). Bezpośrednio po naciśnięciu przez kierowcę pedału hamulca z siłą FPH najpierw powstają tylko: siła hamowania hamulca FHH i generowany przez nią moment hamowania siły hamowania hamulca MFHH (rys. 10a/2). Niezrównoważony moment MFHH hamuje ruch obrotowy koła. Rośnie poślizg koła PK (odcinek wykresu od pkt 2 do 3, rys. 10b), co powoduje wzrost wartości współczynnika tarcia wzdłużnego opony mW. W konsekwencji rosną wartości siły hamowania FH i momentu siły hamowania MFH (rys. 10a/2-3). Wzrost poślizgu koła PK i współczynnika tarcia wzdłużnego opony mW trwa do chwili osiągnięcia równowagi momentu siły hamowania MFH i momentu hamowania siły hamowania hamulca MFHH (rys. 10a/3). Wówczas hamowanie odbywa się w warunkach równowagi, a wartość współczynnika tarcia wzdłużnego opony mW dla aktualnej wartości poślizgu koła PK oznacza pkt 3 wykresu na rys. 10b.
W drugim z omawianych przebiegów hamowania kierowca najpierw kontynuuje hamowanie w warunkach równowagi momentu siły hamowania MFH i momentu hamowania siły hamowania hamulca MFHH (rys. 11a/3). Wartości współczynnika tarcia wzdłużnego opony mW dla aktualnej wartości poślizgu koła PK oznacza pkt 3 wykresu na rys. 11b. Kierowca nagle zwiększa siłę nacisku na pedał hamulca FPH, aby zwiększyć siłę hamowania pojazdu. Bezpośrednio po naciśnięciu przez kierowcę pedału hamulca z większą siłą FPH (rys. 11a/4) zwiększają się: siła hamowania hamulca FHH i generowany przez nią moment hamowania siły hamowania hamulca MFHH. Początkowo nie zmieniają się: poślizg koła PK, a więc również współczynnik tarcia wzdłużnego opony mW (pkt 4 wykresu, rys. 11b).
Po ułamkach sekund niezrównoważony moment hamowania siły hamowania hamulca MFHH zaczyna hamować ruch obrotowy koła, co powoduje wzrost poślizgu koła PK, a w następstwie współczynnika tarcia wzdłużnego opony mW (od pkt 4 wykresu, rys. 11b). Rosnący współczynnik tarcia wzdłużnego opony mW osiąga wartość maksymalną (pkt 5 wykresu, rys. 11b). W konsekwencji również siła hamowania FH i moment siły hamowania MFH osiągają wartości maksymalne, mimo tego moment siły hamowania MFH nie jest w stanie zrównoważyć momentu hamowania siły hamowania hamulca MFHH (rys. 11a/5).
Niezrównoważony moment hamowania siły hamowania hamulca MFHH powoduje dalszy wzrost poślizgu koła PK, ale – jak widać na wykresie na rys. 11b – odcinek wykresu pomiędzy punktami 5 i 6 maleje wartość współczynnika tarcia wzdłużnego opony mW w porównaniu do wartości maksymalnej osiągniętej w pkt 5.
W konsekwencji:
- nie zostaje osiągnięty stan równowagi pomiędzy momentem siły hamowania MFH i momentem hamowania siły hamowania hamulca MFHH;
- poślizg koła PK osiąga wartość równą 100% (pkt 6 wykresu, rys. 11b);
- zablokowane, nieobracające się koło jest hamowane siłą hamowania FH (rys. 11a/6), której wartość jest zależna od wartości współczynnika przyczepności wzdłużnej opony mW dla koła zablokowanego (pkt 6 wykresu rys. 11b).
W chwili gdy doświadczony kierowca zorientuje się, że koło jest zablokowane (pkt 6 wykresu, rys. 12b), powinien spowodować jego odblokowanie, bez przerywania hamowania. W celu odblokowania nieobracającego się koła (rys. 12a/6) kierowca zmniejsza siłę nacisku na pedał hamulca FPH (rys. 12a/7). W pierwszej chwili zmniejsza się moment hamowania siły hamowania hamulca MFHH (rys. 12a/7), ale koło pozostaje nadal zablokowane (pkt 7 na wykresie, rys. 12b). Następnie niezrównoważony moment siły hamowania MFH powoduje, że koło zaczyna się ponownie obracać, a poślizg koła PK maleje (od pkt 7 wykresu, rys. 12b).
Kierowca powinien tak zmniejszyć nacisk na pedał hamulca, aby wartość współczynnika tarcia wzdłużnego opony mW najpierw osiągnęła wartość maksymalną (pkt 8 wykresu, rys. 12b), a następnie zmalała (pkt 9 wykresu, rys. 12b), tak aby hamowanie przebiegało w warunkach równowagi momentów: MFH – pochodzącego od siły hamowania FH i MFHH – pochodzącego od siły hamowania hamulca FHH (rys. 12a/9).
W ten sposób postąpi doświadczony kierowca. Trudno mu jednak jednocześnie kontrolować zachowanie wszystkich kół pojazdu i regulować wartość siły hamowania oddzielnie dla każdego z nich. Jeśli reguluje, to jednocześnie wszystkich kół pojazdu. Mniej doświadczony kierowca, jeśli w ogóle zorientuje się, że któreś z kół jest zablokowane, przerwie na chwilę hamowanie (wszystkich kół), by zacząć je ponownie. Jak dowiemy się później, układ ABS ma przewagę nad tymi rodzajami kierowców.
Zakres stabilny i niestabilny hamowania
Na wykresie, który przedstawia zależność wartości współczynnika tarcia wzdłużnego opony mW od poślizgu koła PK (rys. 13) typową dla nawierzchni innych niż sypkie, wyróżnia się dwa zakresy hamowania: stabilny i niestabilny.
Zakres hamowania stabilnego to hamowanie w zakresie wartości poślizgu koła PK:
- od PK = 0, przy którym koło toczy się bez poślizgu (punkt T),
- do wartości PK(mWMAX), przy którym współczynnik tarcia wzdłużnego opony mW osiąga wartość maksymalną (punkt O).
W zakresie stabilnym hamowania wzrost wartości poślizgu koła PK powoduje wzrost wartości współczynnika tarcia wzdłużnego opony mW. Dzięki tej zależności w tym zakresie możliwe jest uzyskanie i utrzymania hamowania w warunkach równowagi (rys. 9). Pokazuje to rys. 10.
Zakres hamowania niestabilnego to hamowanie w zakresie wartości poślizgu koła PK:
- od wartości PK(mWMAX), przy którym współczynnik tarcia wzdłużnego opony mW osiąga wartość maksymalną (punkt O),
- do PK = 100%, przy którym koło jest zablokowane.
W zakresie niestabilnym hamowania wzrost poślizgu koła PK powoduje zmniejszenie wartości współczynnika tarcia wzdłużnego opony mW. Teoretycznie możliwe jest hamowanie stabilne (rys. 9), ale w warunkach rzeczywistych utrzymanie takich warunków hamowania nie jest możliwe. Pokazują to rys. 11 i 12.
Jeśli podczas hamowania układ ABS pracuje, to jego zadaniem jest utrzymanie wartości poślizgu koła PK na granicy pomiędzy hamowaniem stabilnym i niestabilnym. Możliwe jest wówczas uzyskanie maksymalnych wartości współczynnika tarcia wzdłużnego opony mW na nawierzchniach innych niż sypkie.
mgr inż. Stefan Myszkowski







Komentarze (0)